U ovom članku pokušat ćemo razumjeti što je bila motivacija za EPR članak, koji su bili temeljni problemi koji su mučili Einsteina i ostale, kakvu ulogu u tome svemu je imao Bohm i kako je Bell, sa svojim nejednakostima, stavio točku na i (imaginarnog broja u Schrödingerovoj jednadžbi). Pokušati ćemo se približiti što je više moguće originalnim idejama, a da bismo napravili to, potrebno je objasniti okolnosti i motivaciju koji su do toga svega doveli. Također, ti argumenti nisu jednostavni, kao ni razumijevanje Bellovih nejednakosti, koje ćemo (ali jednostavno) matematički i dokazati u tekstu. Ideja je da nakon čitanja ovog članka imate poprilično dobar pregled EPR fenomena kao fundamentalne posljedice kvantne mehanike, bez obzira na eventualno nepoznavanje kvantne mehanike. Također, preporučam da prije čitanja pogledate jedan simpatičan klip o EPR, uvoda i vizualizacije radi. Ako ste baš motivirani da napokon saznate što je taj slavni EPR, ohrabljujem vas da čitate dalje – ukoliko ne, članak će vam dobro doći da spamate suparnike u facebook raspravama vezanih za kvantnu. Samo ga zalijepite u komentar, teško da će vam ga suparnik imati volje čitati.

1. Komunisti, depresivci, ljubavnici i kvantni fizičari

Povijest kvantne mehanike prepuna je nejasnoća i kontroverzi. Naravno, ne onih koje svakodnevno vidite na dnevnim portalima – osim ako ignoriramo Einsteinov incident sa isplaženim jezikom. Od samoga početka kvantne mehanike nije postojalo slaganje oko temelja teorije, te su se vodile brojne diskusije (naročito na Solvayevim konferencijama).

Einstein i Bohr bili su sukobljeni oko temeljnih pitanja kvantne mehanike. Einstein ju je smatrao nepotpunom i prepunom problema, dok je Bohr smatrao da je riječ o konačnoj teoriji kojoj ne trebaju zakrpe i koja nemam nikakvih realnih problema. Einstein je žudio za ontologijom, lokalnosti i čišćom slikom čitave teorije, dok je Bohr bio zaokupljen svojom novom filozofijom komplementarnosti koja mu je pomagala, ne samo da razumije kvantnu mehaniku, nego i čitav svijet oko njega.

Većina poznatih fizičara tog vremena stala je uz Bohrovu stranu, još veća većina se nije opterećivala s tim problemima već je samo tražila od teorije da dade točne rezultate, te je Einstein ostao sam uz neke disidente. A ti disidenti nisu bili nepoznata imena.

Prvi među njima bio je Erwin Schrödinger po kojem centralna jednadžba u nerelativističkoj kvantnoj mehanici nosi ime. Ali i najpoznatija fizičarska mačka. Erwin je, nakon što su mu reinterpretirali valnu funkciju, pobjegao u Irsku i od tamo kritizirao kvantnu mehaniku, baveći se, između ostaloga, i termodinamikom života. Te ženom i ljubavnicom. Istovremeno. (Ah, ta kvantna mehanika). Poručio je urbi et orbi da mu je žao što je imao veze sa kvantnom mehanikom, a što se Bornove interpretacije njegove valne funkcije tiče, u jednom od pisama Albertu Einsteinu je napisao:

Bog zna da nisam prijatelj teorije vjerojatnosti. Mrzio sam je od prvog trenutka kada ju je moj dragi prijatelj Max Born uveo (u kvantnu).  [1]

Još jedan od disidenata koji je stao uz Einsteina bio je i Louis de Broglie, čije je puno ime kompliciranije od njegove jednadžbe za koju je dobio Nobelovu nagradu: Louis-Victor-Pierre-Raymond, 7e duc de Broglie. Ni de Broglie nije bio previše zadovoljan kvantnom mehanikom te ju je pokušao reinterpretirati na način da je uveo “pilot-val teoriju” u kojoj su čestice u kvantnoj vođene određenim “kvantnim valom”.  Tu je ideju prezentirao na petoj Solvayevoj konferenciji 1927. godine, ali ga je Wolfgang Pauli, koji je matematiku imao u malome prstu, toliko iskritizirao da mu više nije padalo spominjati tu ideju.

Pauli će kasnije kritizirati i Davida Bohma, čovjeka koji je napravio sličnu kvantnu teoriju (neovisno o de Brogliu, pošto nije bio svjestan de Broglijeve ideje), ali će mu na te kritike Bohm itekako odgovoriti i obraniti svoju teoriju. Bohm je bio još jedan od poznatih disidenata, ali ne iz tog vremena, on je došao malo kasnije, kao Einsteinov student. Amerikanci su ga proganjali jer su bili uvjereni da je komunist, premda se u bohmovskim kuloarima danas šuška da je na sastanke partije išao prvenstveno radi zgodnih cura koje su se tako okupljale. I hear you, brother. Svo to proganjanje i bijeg iz USA u Brazil (pa onda u UK), ga je učinilo depresivnim – ta depresija se poprilično pogoršala pred kraj njegova života, zbog koje je morao biti i hospitaliziran.

Ni hejter Pauli nije bio najbolje, kada je depresija u pitanju. Imao je više živčanih slomova za života i liječio se kod slavnog psihoterapeuta Carla Junga. Kvantna mehanika je opasna stvar.

A sam Albert Einstein je pobjegao u USA i tamo, zajedno sa još jednim poznatim disidentom, Kurtom Gödelom, koji je također bio stara škola njemačke metafizike (jedan od najvećih logičara u povijesti koji je umro od gladi jer se bojao da će ga netko otrovati), provodio dane na Princeton Institute, pokušavajući ujediniti vlastitu teoriju sa kvantnom mehanikom, te pokušavajući naći način kako da napadne Bohrovu (Kopenhagenšku) kvantnu mehaniku. I taman kad su ga Bohr, Heisenberg, Pauli i ostali otpisali, zadao je, 1935., svoj konačan udarac kvantnoj teoriji.

O tom konačnom udarcu ćemo pisati u ovom tekstu. Ali da biste uistinu shvatili taj “konačan udarac”, ali mislim stvarno stvarno shvatili, a ne kao što se to inače radi kod popularnih članaka, morat ćemo proći kroz neke stvari iz formalizma i temelja teorije.

Tekst će biti dug, no nikakvo matematičko znanje nije potrebno, i na kraju dana ćete znati što je EPR paradoks (fenomen), zašto je nastao i kako je riješen.

I neće biti ovako previše opušten kao ovaj uvod  Ali bit će istinit, što je bitnije.

Pa krenimo.

2. Formalizam

Kvantna mehanika bazira se na određenom broju aksioma. Za kvalitetno razumijevanje EPR fenomena dovoljno je predstaviti dva.

2.1 Prvi aksiom

Valna funkcija predstavlja kompletan opis sistema.

Rješenje Schrödingerove jednadžbe za određeni problem u kvantnoj mehanici je valna funkcija. Kaže se da ta valna funkcija sadrži sve informacija koje možemo znati o kvantnom sistemu – odnosno da ne mogu postojati dodatne informacije koje nisu uključene u valnu funkciju. Postojanje takvog nečega zvalo bi se “skrivene varijable”.

Einstein je ovaj aksiom odbacivao do kraja života, smatrajući da je kvantna mehanika određeno proširenje statističke mehanike i da valna funkcija ne priča o jednom sistemu (kojeg promatramo) nego da predstavlja ansambl slično pripremljenih sistema, te je, stoga, smatrao da je kvantna mehanika nepotpuna  – stoga će mu ovaj aksiom biti jedna od motivacija za EPR članak.

2.2 Drugi aksiom (aksiom mjerenja)

Valna funkcija, kao superpozicija svih mogućih stanja, u kvantnoj mehanici deterministički evoluira u vremenu. Što znači “superpozicija svih stanja”? Recimo da imamo jednostavan sistem u kojem nam se čestica može naći samo u dva stanja  (npr. zamislimo kutiju sa pregradom, nakon sto spustimo pregradu, čestica može biti ili u lijevom dijelu kutije ili u desnom dijelu kutije), tada će taj sistem prije mjerenja biti u superpoziciji ta dva stanja (“lijevo” i “desno”). Međutim, kada izvršimo mjerenje (otvorimo kutiju), mi nećemo naći česticu istovremeno i lijevo i desno, nego ili lijevo ili desno, stoga će valna funkcija (“lijevo+desno”) morati pasti u jedno od mogućih stanja (“lijevo” ili “desno”).

I tu dolazi do drugog aksioma. Prilikom mjerenja sustav iz superpozicije stanja pada u jedno stanje. Uz dva problema koji se nameću: (a) mjerenje nije strogo definiran pojam, (b) nužno je da taj prijelaz bude nelokalan, odnosno da se dogodi “beskonačnom” brzinom.

Potonju opciju je potrebno malo obrazložiti. Vratimo se našoj kutiji, no ovaj put, prije nego je otvorimo, razdvojimo dva dijela kutije i pošaljimo jednu na Mjesec, dok druga ostaje na Zemlji (jer u fizici volimo primjere iz svakodnevnog života). Nakon nekog vremena, otvorimo kutiju na Zemlji i primijetimo da je čestica upravo u toj kutiji. Ako pretpostavimo da (b) nije točno, odnosno da se prijelaz iz “čestica_na_Mjesecu+čestica_na _Zemlji” u “čestica_na_Zemlji” događa nekom konačnom brzinom, to bi značilo da je, kada smo otvorili kutiju na Zemlji i saznali da je tu čestica, trebalo određeno vrijeme da informacija “čestica nije na Mjesecu, nego na Zemlji” dođe do Mjeseca, što bi omogućilo da čestica neko vrijeme bude detektirana na dva mjesta istovremeno, što je u kontradikciji sa eksperimentima.

Einstein je već na Solvayevim konferencijama primijetio da i kod slavnog double-slit eksperimenta dolazi do ovakvog tipa nelokalnosti, kao posljedice aksioma mjerenja, te mu je stoga bila to još jedna motivacija da napadne kvantnu mehaniku preko EPR članka.

Stoga, Einstein smatra da je kvantna mehanika nepotpuna (negira prvi aksiom), te da je nelokalnost koja je posljedica drugoga aksioma pokazatelj da nešto ne valja u kvantnoj mehanici. Stoga će upotrijebiti te dvije informacije da zada svoj posljednji udarac kvantnoj mehanici.

Ako se sjetimo da je Einstein tvorac teorije koja je uvela lokalnost (nista se ne propagira brzinom većom od brzine svjetlosti u vakuumu), jasno je zašto mu je očigledna nelokalnost smetala. Jasno, postojali su i druge stvari koje su Einsteina, pa  i Schrodingera, de Brogliea, itd., smetali oko kvantne, ali u ovom tekstu nećemo ulaziti u njih.

2.3 Komutatori, postojanje i nepostojanje

Samo još jedna mala stvarčica iz kvantne i onda možemo u potpunosti razumjeti EPR. U kvantnoj mehanici operatori (matematički objekti), na neki način, predstavljaju fizikalne veličine (često se  griješi da operator daje vrijednost mjerenja, što je miskoncepcija). Ako dva operatora ne komutiraju (ništa posebno, ako imam dva operatora  A i B i ako vrijedi AB-BA=0, kažemo da komutiraju), kažemo da sistem nema istovremeno definirane dvije fizikalne veličine koje operatori predstavljaju. Npr. operatori pozicije i količine gibanja ne komutiraju, stoga, ako nam operator količine gibanja dade točno definiranu veličinu količine gibanja, opetator pozicije nam neće moći dati točnu poziciju čestice, već tek vjerojatnost da se čestica nađe u određenom regionu.

Kopenhagenška interpretacija, koja je u u jednu ruku “standardna interpretacija kvantne mehanike”, u smislu da se po njoj uči na sveučilištima, eksplicitno tvrdi da, u gore navedenom slučaju, čestica nema poziciju. Dakle, ne samo da ne možemo izračunati njenu poziciju, nego je niti nema, odnosno pozicija nema realnost (dok količina gibanja ima).

Upravo će to biti zadnji element koji će biti potreban Einsteinu da napadne kvantnu mehaniku. Želimo našem Albertu svu sreću da ponovno osvoji srce odbjegle mu kvantne mehanike koja je u to vrijeme provodila dane u hladnom Kopenhagenu, razdvojena između strogog matematičkog formalizma i neobične nove filozofije Nielsa Bohra.

“She looked lonely and I knew the cure
Old memories would win her heart for sure
I thought I’d walk on in
And I give it my best shot.”

3. Einstein-Podolsky-Rosen fenomen

Pokušajmo razumjeti argumente iz EPR članka. No prije nego išta napišemo, naglasimo jednu prešutnu pretpostavku, a to je lokalnost. Odnosno da se nikakvi procesi u prirodi ne događaju beskonačnom brzinom, točnije, da ništa ne može da se kreće brzinom većom od brzine svjetlosti u vakuumu.

Albert Einstein je, zajedno sa suradnicima Borisom Podolskim i Nathanom Rosenom, 1935. godine zadao svoj posljednji udarac kvantnoj mehanici sa člankom pod nazivom “Can quantum-mechanical description of physical reality be considered complete?” [2].  U to vrijeme takve stvari su bile sexy, pa je Podolsky otišao do redakcije New York Timesa, a oni su, i prije nego što je originalni članak bio objavljen, na naslovnici novina objavili članak o tome kako Einstein napada kvantnu teoriju! Naravno da je Einstein to kasnije saznao, naljutio se i više nikad nije surađivao sa mladim američko-ruskim fizičarem.

3.1 Argumenti EPR članka

Članak započinje sljedećim riječima:

U potpunoj teoriji postoji element koji odgovara odgovara svakom elementu realnosti. Dovoljan uvjet za realnost neke fizičke vrijednosti je mogućnost predviđanja takve vrijednosti sa sigurnosti, bez poremećaja sistema. U kvantnoj mehanici, u slučaju dvije fizikalne vrijednosti opisane sa nekomutirajućim operatorima, poznavanje jedne fizikalne vrijednosti isključuje poznavanje druge. Tada nam ostaju dvije mogućnosti:

(1) Ili opis realnosti preko valne funkcije nije potpun,

(2) Ili Fizikalne vrijednosti nekomutirajućih operatora ne mogu imati istovremenu realnost.

 

EPR argument se svodi na to da se pretpostavi da je (1) netočno i pokaže da iz toga slijedi kako je i (2) netočno, stoga nam jedino preostaje prihvaćanje (1) kao točnoga.

Zbunjeni ste, je l’ da? Zahvalite Rosenu na njegovoj ideji postavljanja ovog problema, Einstein je imao na umu nešto puno jednostavnije, a to se može svesti na ovo: ako pokažemo da nekomutirajući operatori (dvije fizikalne veličine) mogu istovremeno imati realnost (čemu se protivi kvantna mehanika), to znači da naše razumijevanje kvantne mehanike nije potpuno, odnosno da valna funkcija nije potpun opis prirode.

Zamislimo sustav od dvije čestice u kojem je očuvana relativna pozicija i ukupna količina gibanja. To znači da ukoliko znamo poziciju jedne čestice, automatski poznajemo poziciju druge, kao i ukoliko poznajemo količinu gibanja jedne čestice, automatski poznajemo i količinu gibanja druge. Takav sustav može se predstaviti spregnutom valnom funkcijom:

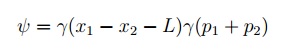
Gdje su x1 i x2 pozicije prve i druge čestice, L udaljenost među njima koje su prevalile čestice prije nego smo izvršili mjerenje, te p1 i p2 količine gibanja prve i druge čestice. U principu, L može biti prozivljno velik. Za potrebe bombastičnosti ovog članka pretpostavimo da je L=93 milijarde svjetlosnih godina (promjer vidljivoga svemira), sa dva promatrača koji stoje na rubovima svemira kao na slici:

 3.2 Mjerenje pozicije

Nazovimo lijevog promatrača Ana, a desnoga Bobo (iz istoimene čuvene sinkronizacije Gospodara prstenova). Ana je mogla odlučiti da mjeri poziciju lijeve čestice (koja je došla do nje). Ne kažemo da je mjerila, nego je u principu mogla mjeriti. U tom slučaju valna funkcija bi iz stanja superpozicije pala u stanje točno određene pozicije (x1) – sjetimo se aksioma mjerenja – a Ana bi odmah znala i poziciju druge čestice (x2) zbog očuvanja relativne pozicije. Međutim, ništa što je Ana učinila ne bi trebalo utjecati na Bobinu česticu, pošto je Bobina čestica daleko od bilo kakvog utjecaja od strane Ane (jer su previše daleko jedna od druge), stoga je Bobina čestica morala imati točno definiranu poziciju, neovisno o tome što je Ana napravila.

3.3 Mjerenje količine gibanja 

Međutim, Ana je umjesto pozicije vrlo lako mogla odabrati da mjeri količinu gibanja svoje čestice. U tom slučaju, zbog zakona očuvanja količine gibanja, Ana bi automatski znala količinu gibanja Bobine čestice. Opet, ništa što je Ana radila nije moglo utjecati na stanje Bobine čestice, koja je na drugome kraju svemira, stoga je Bobina čestica, u principu, morala imati unaprijed definiranu količinu gibanja koju je Ana, svojim mjerenje, otkrila.

Stoga, ako u principu Ana može birati da izmjeri točnu poziciju ili količinu gibanja Bobine čestice, a ako istovremeno ne može utjecati na Bobinu česticu jer je previše udaljena od Anine, nameće se da su vrijednosti pozicije i količine gibanja bile već unaprijed definirane i da moraju sadržavati točnu vrijednost.

3.4 Zaključak

U oba slučaja, ništa što je radila Ana nije moglo utjecati na Bobinu česticu, stoga je Ana, mjereći poziciju ili količinu gibanja, otkrila nešto što je već postojalo kod Bobine čestice. Međutim, pozicija i količina gibanja su nekomutirajući operatori, a (Kopenhagenška) kvantna mehanika tvrdi da te dvije fizikalne veličine ne bi smjele imati istu realnost; ali ovaj primjer, sa jako razdvojenim česticama (space-like separation), upravo daje protuprimjer, gdje pozicija i količina gibanja istovremeno imaju istu realnost (odnosno za Bobinu česticu postoji količina gibanja i pozicija, istovremeno).

Stoga je EPR članak pokazao da ukoliko pretpostavimo da je opis realnosti preko valne funkcije potpun (tj. da (1) nije točno), možemo pokazati da fizikalne vrijednosti nekomutirajućih operatora  mogu imati istovremenu realnost (tj. da ni (2) nije točno), odnosno, ako (1) nije točno, ni (2) nije točno.

Što nas vodi zaključku da je (1) točno, odnosno da opis realnosti preko valne funkcije nije potpun.

3.5 Goodbye Moonmen

Naš Albert mogao je biti zadovoljan. Pokazao je da kvantna mehanika, odnosno njen formalizam, uz više nego racionalnu pretpostavku lokalnosi, daje rezultate koji ukazuju na to da je kvantna mehanika nepotpuna teorija. Einstein je rekao svoje i mogao je ići. Još će pisati o ovom problemu, u okviru raznih drugih čanaka, ali tu je dosego svoj vrhunac. Dva desetljeća kasnije, doktori će mu reći da mora na operaciju, na što će Einstein, gentlemanski, ustvrditi kako je bezukusno da umjetno produljuje život, da je odradio svoje i da je vrijeme da ode – elegantno. Three, point, one, four, one, five, alive no longer my amour, faded for home May of ’54.. odnosno April ’55.

4. Bohm – Aharonov EPR

Godine 1957. David Bohm, zajedno sa Yakir Aharonovim, objavljuje članak “Discussion of experimental proof for the paradox of Einstein, Rosen, and Podolsky” [3] u kojem radi prvi korak mogućnosti eksperimentalnog testiranja EPR fenomena. Bohm i Aharonov predstavili su EPR fenomen u, konceptualno lakšem i eksperimentalno realističnijem, ruhu singlet stanja. Singlet stanje je stanje dvije čestice u kojemu ukupan spin mora biti jednak nuli. Nešto o takvim valnim funkcijama smo pisali ovdje.  Takva valna funkcija izgleda ovako

Ona govori sljedeće: ukoliko prva čestica ima spin “gore”, druga će imati spin “dolje” i obratno. Naravno, kada bi klasična mehanika bila u pitanju, stvar bi bila jednostavna – rekli bismo da su čestice od početka imale definiran spin (gore ili dolje), a da smo mjerenjem samo otkrili koja je čestica bila u stanju spina “gore”, a koja u stanju spina “dolje”. Međutim, to kvantnomehanička valna funkcija ne govori. Ona govori da je sustav u “miješanom” stanju (superpozicija svih stanja) i da mjerenjem (aksiom mjerenja) prelazi u jedno od mogućih stanja (gore ili dolje). Stoga, prije samoga mjerenja, čestice ne bi trebale imati definiran spin.

Komponente spina su, baš kao pozicija i količina gibanja, nekomutirajuće veličine. Odnosno, ako poznajemo jednu komponentnu (npr. spin u smjeru z-osi), ostale dvije komponente nemaju definiranu vjernosti, stoga, po Kopenhagenu, nemaju realnost (ne postoje).

Međutim, ako i ovaj sustav dovoljno separiramo (separibilnost), dovoljno daleko da možemo reći da ono što radimo na prvoj čestici nije imalo dovoljno vremena da utječe na drugu česticu, tj. ako pretpostavimo da ono što radimo jednoj čestici ne može utjecati na drugu česticu (lokalnost), imamo isti problem kao i kod EPR-a.  Ponovno, u načelu, možemo odlučiti da kod Anine čestice mjerimo z-komponentu spina i automatski poznajemo z-komponentu spina Bobine čestice (ako je Anina “gore”, Bobina je “dolje”). Ali Ana je u načelu mogla mjeriti y-komponentu ili x-komponentu spina i dobiti automatski y- i x-komponentu spina Bobine čestice. Ponovno, kako su te čestice dovoljno razdvojene, ništa što je učinila Ana ne bi smjelo utjecati na stanje Bobine čestice, stoga smo prisiljeni zaključiti da je Bobina čestica imala sve komponente spina, bez obzira na nekomutiranje, odnosno da je opis stvarnosti valnom funkcijom nepotpun.

4.1 Prve naznake nelokalnosti

Bohm i Aharonov uzimaju kvantnu mehaniku ozbiljno, te, smatrajući da će budući eksperimenti pokazati da formalizam kvantne mehanike daje točne rezultate, analiziraju što bi to značilo.  Iz kvantne mehanike znamo sljedeće tri činjenice:

(1) Samo je jedna komponenta spina (i to ona koju odlučimo mjeriti!)  čestice može imati definiranu vrijednost, dok su ostale komponente nasumične fluktuacije.
(2) Bez obzira koju komponentu prve čestice mjerimu, ista komponenta druge čestice će uvijek imati definiranu vjernost, samo u suprotnom smjeru (tj. ako je z-komponenta spina prve čestice “gore”, z-komponenta spina druge čestice će biti “dolje”).
(3) Imamo slobodu da izaberemo bilo koji smjer koji želimo mjeriti i koji god da smjer izaberemo, uvijek će baš u tom smjeru spin čestice biti definiran, dok u ostalima neće.

Ako, ponovno, razdvojimo dvije čestice (dovoljno daleko) i ako Ana mjeri spin svoje čestice  u smjeru z, ona će tim mjerenjem utjecati na x- i y-komponentu spina svoje čestice,  na način da će se te komponente naći u nedefiniranom stanju (imati će određnu vjerojatnost da imaju određeno stanje, za razliku od z-komponente spina koje će imati točno određeno stanje). Mjerili smo sustav, poremetili smo ga i imamo neodređenost. Dobro, možemo to prihvatiti – ne zvuči nimalo čudno, naročito ako uzmemo da nam je aparat makroskopski, a sistem mikroskopski. Međutim, kako objasniti zašto se Bobina čestica odlučila ponašati na isti način? Bobina čestica je također odlučila da ima definiranu vrijednost z-komponente spina, a nedefinirane vrijednosti x- i y- komponenti, a toliko je udaljena od Ane da informacija o tome da je Ana bilo šta radila ne može doći dovoljno brzo do Bobine čestice, da je obavijesti o tome.

Takvo ponašanje se jedino može objasniti ako pretpostavimo da ta dva sustava nekako komuniciraju bez obzira što su razdvojeni i da je ta komunikacija trenutna, odnosno da se odvija beskonačnom brzinom – što je svakako u kontradikciji sa teorijom relativnosti.  Stoga Bohm i Aharonov zaključuju:

Netko bi mogao pretpostaviti da postoji nekakva skrivena interakcija između B i A ili između B i mjernog aparata, koja bi objasnila ovakvo ponašanje. Takva interakcija bi bila, u najmanju ruku, van okvira trenutne kvantne teorije. Štoviše, bila bi trenutna, pošto se smjer mjernog aparata može brzo promijeniti, te bi spin B čestice morao reagirati odmah na takvu promjenu. Takva interakcija između udaljenih sistema općenito ne bi bila konzistentna sa teorijom relativnosti. Ovaj rezultat predstavlja esenciju paradoksa od Einsteina, Rosena i Podolskoga.

5. Eksperimenti

Eksperimenti sa EPR fenomenom se uglavnom rade sa parom fotona (s polarizacijom u okomitim smjerovima), pošto je takav eksperiment tehnički najjednostavnije izvesti. No da se bezrazložno ne prebacivamo na novu valnu funkciju (dva fotona okomitih polarizacija kao pobuđenja polja), možemo slobodno ostaviti sliku singlet stanja dva (spina) elektrona. Eksperiment izgleda otprilike ovako [4]:

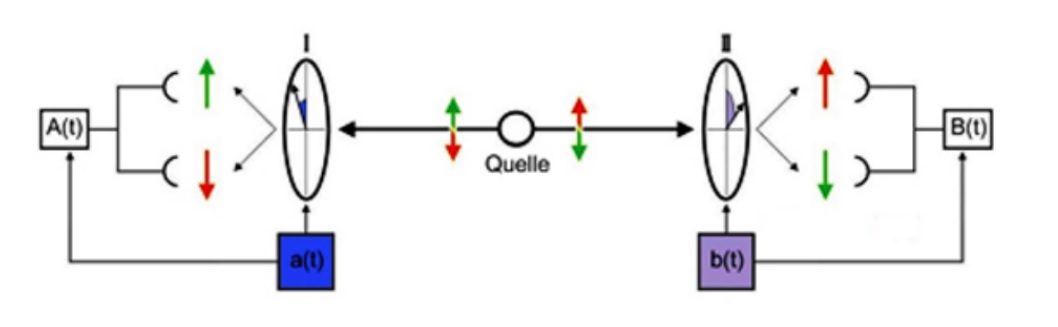
U sredini je izvor (Quelle, njem. izvor) koji producira par čestica. Primijetite odmah desno i lijevo od izvora stoje nekakve dvije strijelice. One označavaju superpoziciju “gore-dolje” spinova za svaku česticu (dakle, čestica nije u  točno određenom stanju ili bar to mislimo). Čestice istovremeno dolaze do detektora spina (zapravo u ovom slučaju polarizacije, ali, ponavljam, to nije toliko važno za razumijevanja fenomena). Detektori zauzimaju nasumičnu poziciju s kojom upravljaju uređaji a(t) i b(t) (ovo “t” znači da su funkcija vremena, tj. da mjenjaju položaj u vremenu). Detektor može detektirati samo dvije moguće vrijednosti: ili “gore” ili “dolje”.

Kvantomehaničkim formalizmo možemo dobiti da je vjerojatnost da će rezultati mjerenja biti točno obrnuti jedan od drugoga (tj. ako je prva čestica orijentirana “gore”, da je druga čestica “dolje” i obrnuto) definirana ovom jednostavnom formulom:

Gdje je θ kut između smjera dva detektora. Primijetimo da ako je taj kut jednak nuli, tj. ako su detektori postavljeni u istom smjeru, dobivamo da je P=1 da rezultati budu obratni, tj. da u tom slučaju, ako je rezultat mjerenja A čestice spin “gore”, B čestica će sigurno imati spin “dolje” i obrnuto. Za ostale kutove to nije tako. Npr. ako je kut između dva detektora 120°, vjerojatnost da će rezultat mjerenja spinova dati suprotne rezultate je 1/4 (odnosno u 4 mjerenja, takvo nešto će se desiti samo jednom).

Ova formula, kao predviđanje kvantnomehaničkog formalizma je, eksperimentalno povrđen fenomen. Detalje eksperimenta možete vidjeti ovdje, tj. referenca [5].

6. Dva moguća objašnjenja EPR fenomena

S obzirom da su rezultati mjerenja kod dva detektora, koja mogu u principu biti odvojena milijunima svjetlosnih godina, korelirana, ostaju nam dvije mogućnosti:

(i) Ili su čestice imale unaprijed definirane vrijednosti (svaka čestica imala je točno određen vriejdnost spina u svakom smjeru, prije mjerenja) i onda smo te vrijednosti u trenutku mjerenja otkrili;

(ii) Ili su čestice dobile određene vrijednosti spina tek u trenutku mjerenja (tj. kada smo prvoj čestici izmjerili spin “gore”, druga se odmah našla u stanju spina “dolje”).

U slučaju (i) valna funkcija nije potpun opis prirode jer ne predviđa postojanje unaprijed definiranih vrijednosti (spina), a u slučaju (ii) priroda je nelokalna, pošto nešto što je, u principu, na jednom kraju svemira, može trenutno utjecati na nešto što je na drugom kraju svemira

7. Jed(i)no točno objašnjenje: Bellova nejednakost

Johna Stewarta Bella zanimalo je sljedeće pitanje: mogu li rezultate kvantne mehanike reproducirati na način da pretpostavim da su naše čestice od početka imali definiranu vrijednost (spina, količine gibanja, itd.), odnosno ako pretpostavimo da je objašnjenje (i) točno, te da čestice nisu mogle međusobno komunicirati (lokalnost). Ukoliko je to moguće, objašnjenje (i) bi nam se nametnulo kao rješenje ovog problema.

U svome članku “On the Einstein-Podolsky-Rosen Paradox” [6] iz 1964. John Bell je matematički dokazao da je takvo što nemoguće. Nemoguće je naći set početnih vrijednosti spina koji bi, uz pretpostavku lokalnosti, reproducirao rezultate kvantne mehanike.

No kao što moto Royal Society of London kaže – nikome ne treba vjerovati na riječ (lat. Nullius in verba) – pa tako ni meni kad vam kažem da je to Bell dokazao. Stoga ćemo radije izvesti taj dokaz. Naravno, originalni dokaz bi premašio pristojnost jednostavnosti popularnog članka, no možemo, na manje generalan način, pokazati da je nemoguće naći kombinaciju početnih vrijednosti spina koje bi reproducirali rezultate kvantne mehanike. I to tako da ćemo se nadovezati na primjer eksperimenta koji smo nešto prije spomenuli.

Dakle, vratimo se na našu formulu za vjerojatnost da je će nam eksperiment dati suprotne rezultate je:

Sada uzmimo da naši detektori mogu mjeriti samo tri smjera (umjesto beskonačno mnogo smjerova) i da su ta tri smjera razdvojena sa kutem od 120° između svakog smjera, kao na slici

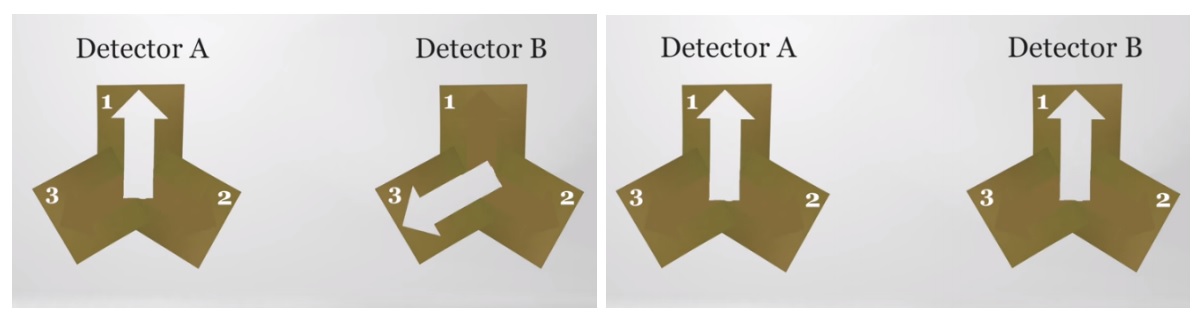
U ovom našem jednostavnijem slučaju postoje samo dvije mogućnosti eksperimentalne konfiguracije:

(a) kada su detektori orijentirani u istom smjeru (desna slika, gore);
(b) kada su detektori orijentirani tako da je kut između njih 120° (lijeva slika, gore).

U slučaju (a) vjerojatnost da će čestice biti u stanju suprotnih spinova je P=1 (sigurno će biti suprotni), dok je u slučaju (b) P=1/4, što smo već ustvrdili ranije.

Sada pretpostavimo da su vrijednosti spina bile definirane prije mjerenja, od samoga početka. Pošto mjerimo samo tri smjera, pretpostavljamo da je svaka čestica imala definiranu vrijednost spina u svakom od tri smjera. Pošto spin ima samo dvije vrijednosti (“gore” ili “dolje” – no u ovom slučaju ćemo ih označiti sa +1 i -1, radi lakšeg snalaženja), mogu postojati tek 2^3 kombinacija početnih vrijednosti spina za jednu česticu, i to:

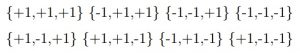
Ovo vam je već sasvim dovoljno informacija da zavrtite mali program i pokušate (neuspješno) sa ovim setom početnih vrijednosti reproducirati (a) i (b). No mi ćemo to, na jednostavan matematički način, dokazati.

Prije nego krenemo, samo ćemo definirati nomenklaturu. Slovo Z  označava vrijednost spina, indeksi a,b,c označavaju tri moguće smjera detekcije, dok natpis 1,2 označavaju prvu i drugu česticu.

Vratimo se sada na naš problem. S obzirom da imamo damo tri mogućnosti početnih vrijednosti, barem dvije od njih moraju biti međusobno jednake, odnosno, barem jedna ova tvrdnja mora biti točna:

Ovo su ništa drugo nego tri tvrdnje o spinovima jedne čestice. Prva zagrada tvrdi da je spin prve čestice u smjeru a jednak spinu iste čestice u smjeru b, itd. Stoga suma vjerojatnosti od ta tri događaja mora biti veći od jedan (pošto smo sigurni da je jedna opcija točna, stoga je njena vjerojatnost već P=1 i to je najmanja moguće vrijednost koje zbroj ove tri vjerojatnosti može imati), te imamo nejednakost:

Međutim, iz (a) znamo da vrijednosti spina dvije čestica u istom smjeru moraju biti obratne, odnosno da je

Iz toga slijedi

Gdje su α i β samo generalne oznake sa bilo koji od mogućih smjerova. Ovaj rezultat vratimo u našu nejednakost

No sada se sjedimo da je vjerojatnost da dvije čestice imaju suprotne smjerove kada je kut između njih jednak 120°, točno P=1/4. A upravo u ovom formuli imamo takvu situaciju u svakom članu (npr. u prvom članu imamo vjerojatnost da dvije čestice imaju različite – odnosno suprotne – vrijednosti u smjerovima a i b,  ti smjerovi su razmaknuti za točno 120°), stoga je

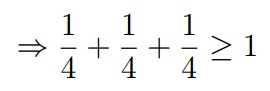
Što je netočno. Odnosno pokazali smo da uz pretpostavku lokalnosti česticama nije moguće pripisati set početnih vrijednosti koje bi reproducirale rezultate kvantne mehanike. [7]

Dakle, ako su rezultati kvantne mehanike točni, a eksperimentalno je potvrđeno da jesu, nije ih moguće reproducirati na način da pretpostavimo da je mjerenje otkrilo već postojeće vrijednosti (spina), odnosno da nije bilo utjecaja jednog sistema (mjerenje jedne čestice), na drugi (lokalnost).

Naravno, taj rezultat ne eliminira skrivene varijable iz kvantne teorije, pošto je čitav izvod nejednakosti baziran na pretpostavci lokalnosti, odnosno da ništa nije moglo utjecati na početne vrijednosti (spinova) jednom kada se sustav razdvojio (kada su dvije čestice otišle do svojih detektora). Ono što nejednakosti eliminiraju je lokalnost, pošto sa takvom pretpostavkom ni na koji način ne možemo reproducirati ovakve rezultate. S druge strane, vi možete imati “skrivene varijable” unutar nelokalne teorije i moći ćete reproducirati rezultate kvantne mehanike (npr. u Bohmovoj mehanici).

8. Zaključak

Vidjeli smo da su brige Einsteina od nelokalnosti u kvantnoj teoriji i kompletnosti iste dovele do slavnog EPR članka u kojemu je pokušao dokazati da je kvantna mehanika nepotpuna. Njegova argumentacija je, uz pretpostavku lokalnosti, točna. Ako pretpostavimo lokalnost, nameće se zaključak da su prije mjerenja postojale (skrivene) definirane vrijednosti raznih fizikalnih veličina (kao količine gibanja, spina, itd.), a pošto valna funkcija ništa ne govori o tome, zaključak je da ona nepotpuno objašnjenje kvantne mehanike. Determinizam je, u tom slučaju, samo posljedica lokalnosti teorije. U to vrijeme teško da je tko sumnjao da je lokalnost netočna pretpostavka, naročito ne Einstein koji se proslavio građenjem teorije koja je maknula nelokalnosti iz Newtonove teorije gravitacije (Opća teorija relativnosti).

U vrijeme objave EPR članka, na način na koji je to Einstein zamislio, bilo je nemoguće eksperimentalno provjeriti njegov misaoni eksperiment. Godinama kasnije Bohm i Aharonov su napravili eksperimentalno prijateljske verzije EPR-a sa spinom i polarizacijom. To je otvorilo vrata za eksperimentalnu provjeru ovog fenomena.

John S. Bell je uzeo Einsteinove argumente ozbiljno, te se zapitao, ukoliko je priroda lokalna i ukoliko postoje već definirane vrijednosti spina prije mjerenja, da li je moguće naći neki skup tih vrijednosti koje bi reproducirale rezultate kvantne mehanike. Bellove nejednakosti dokazuju da je takvo što nemoguće.

Sjetimo se da su nam na stolu bile dvije mogućnosti:

(i) Ili su čestice imale unaprijed definirane vrijednosti (svaka čestica imala je točno određen vriejdnost spina u svakom smjeru, prije mjerenja) i onda smo te vrijednosti u trenutku mjerenja otkrili;
(ii) Ili su čestice dobile određene vrijednosti spina tek u trenutku mjerenja (tj. kada smo prvoj čestici izmjerili spin “gore”, druga se odmah našla u stanju spina “dolje”).

S obzirom da je Bell pokazao da je (i) nemoguće, ostala nam je samo opcija (ii). Kvantna mehanika je nelokalna teorija, odnosno priroda je nelokalna.

Ili, primjerom rečeno, možemo imati situaciju u kojem su dvije čestice beskonačno udaljene i ukoliko “nešto napravite” prvoj čestici, druga čestica će to odmah “osjetiti”. Odmah.

Što će vam science-fiction pored kvantne teorije?

9. Je li Bell dokazao nešto što nije dokazao?

Osim što je to jasno iz njegovih radova, Bell je bio prisiljen eksplicitno tvrditi da je dokazao to što je dokazao jer su već i tada, kao i sada, pojedini fizičari tvrdili da je dokazao nešto što sam Bell nije smatrao da je dokazao. Za takve rasprave vidjeti reference [8,9].

Te tvrdnje su išle toliko daleko, da su neki smatrali da je Bell falsificirao sve teorije koje u sebi sadrže “skrivene varijable” (bez obzira na nelokalnost), kao što je to Bohmova mehanika. Da bi ironija bila veća, Bell je bio zagovornik Bohmove mehanike i čak mu je ona bila inspiracija za njegove nejednakosti.

Međutim takve miskoncepcije toliko daleko idu, da se mogu naći i u izvješćima National Science Foundation [10]

I miskoncepcija će biti. I to je u redu. Netko će pokušati sve to objasniti sa retrokauzalnosti [11], što nije miskoncepcija i lijepo je za vidjeti da postoji takva mogućnost, ali još je daleko od objašnjenja.  Netko će i dalje tvrditi da Bell nije znao što je dokazao, a netko će u tome vidjeti dokaz da Bohmova mehanika nije točna. Netko će reći da sa kvantnom mehanikom nema nikakvih problema jer je mogu promijeniti u labosu bez ikakvih poteškoća, netko će reći da aksiom mjerenja ne zahtjeva dublje objašnjenje, točnije izvod, dok će nekima “mjerenje” biti sasvim opravdan i precizan pojam unutar kvantne mehanike (koliko god neprecizan bio i koliko god je nejasno kada i kako se to “mjerenje” događa). Nekima su Bellove nejednakosti dokaz da kvantna mehanika nije “klasična teorija”, a nekima je Einstein u stare dane bio stara budala koja je pisala gluposti o kvantnoj jer je nije razumjela (gluposti citirane više od 14 000 puta)..

I to je sve u redu.

Kako bi Grace Slick rekla:

“And if people don’t seem to like it that’s O.K. – let ‘em go
Some day they’ll sing a song of their own.”

A s tom bi pjesmom završio ovaj članak.

Jer ako ste izdržali do ovdje, onda ste stvarno zaslužili jednu dobru staru stvar..

REFERENCE

[1] Letter to Albert Einstein (13 June 1946), as quoted by Walter Moore in Schr¨odinger: Life and Thought (1989)

[2] A. Einstein, B. Podolsky, and N. Rosen. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?, Phys. Rev. 47, 777 (1935).

[3] Bohm, D., and Y. Aharonov, 1957, Discussion of Experimental Proof for the Paradox of Einstein, Rosen and Podolski, Physical Review, 108: 10701076.

[4] Reinhold A. Bertlmann. Theoretical Physics T2 Quantum Mechanics (script). URL: http://homepage.univie.ac.at/reinhold.bertlmann/pdfs/T2Skriptfinal.pdf

[5] Alain Aspect, Philippe Grangier, and Grard Roger. Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities, Phys. Rev. Lett. 49, 91 (1982)

[6] Bell, J. S., 1964, On the Einstein-Podolsky-Rosen Paradox, Physics, 1: 195200, reprinted in Bell 1987

[7] http://www.scholarpedia.org/article/Bell’stheorem

[8] Werner, R.F. Comment on ’What Bell did’, J. Phys. A: Math. Theor.47 424011, 2014

[9] Maudlin, T.W. Reply to Comment on ’What Bell did’, J. Phys. A: Math. Theor.47 424012, 2014

[10] Cushing, J.T. review of Bohm, D., and Hiley, B., The Undivided Universe, Foundations of Physics, 25, 507, 1995

[11] Richard Corry. Retrocausal models for EPR, Studies in History and Philosophy of Science Part B, Volume 49, 19 (2015).